Image processing module¶

class app.imgprocessing.segmentation.Segmentation[source]¶

This class provides the methods to reduce and segment the images of the toy model. It assumes that the set of Dicom files that represents the toy model have been tranformed in an array of numpy.

reduction(img, factor=0.2222222222222222)[source]¶

This method reduces the set of images of the toymodel by a given scale factor or zoom factor, using the C-Spline algorithm which is provided by the ndimage module of scipy

C-Spline algorithm consists in funding a function which is the linear combination of piecewise definened functions known as Basis Splines (B-Splines), which are smooth functions whose first, second and third derivative pass through one point of the given discrete set:

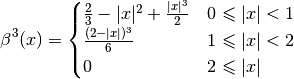
$\beta ^3(x) =\begin{cases} \frac{2}{3} - |x|^2 + \frac{|x|^3}{2} & 0\leqslant |x|< 1 \\ \frac{(2-|x|)^3}{6} & 1\leqslant |x| < 2 \\ 0 & 2\leqslant |x| \end{cases}$

The linear combination of the B-Spline functions can be expressed by the next equation:

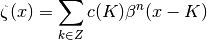
$\zeta (x) = \sum _{k\in Z} c(K)\beta ^n(x-K)$

Parameters:	img (3d numpy array) – representation of the toy model factor (float) – zoom factor in which the image is reduced
Returns:	the image rescaled
Return type:	3d numpy array

view(original, segmented, reduced)[source]¶: This method is implemented for test purposes, it takes as arguments an untreated slice, a segmented slice and a reduced and segmented slice showing its differences on screen using a matplotlib figure

view(original, segmented, reduced)

histogram(img_red)[source]¶: Plots an histogram of the materials distibution over the toy model using matplotlib. It is neccesary to reduce the toy model before plotting the histogram. For test porpuses

histogram(reduced_toymodel)

clasify(img, normalize=True, n_clusters=3)[source]¶

This method segments or clasify the values of the given image in three different groups of values, thus the different Hounsfield unit values found in the image are replaced by only three different values. If the parameter normalize is true, these values are:

0 for the air-void
1 for the mastic
2 for the aggregates

For this porpuse, a implementation of the K-means algorithm, provided by the cluster module of the Scikit-learn library, is used. K-means algorithm takes a dataset X of N values, and a parameter K specifies how many cluster to create. K-means finds evenly-spaced sets of points in subsets of Euclidean spaces called Voronoi diagrams. Each found partitions will be a uniformly shaped region called Voronoi cell, one for each material. This process is executed in two steps:

The assign step consists in calculating a Voronoi diagram having a set of centroids 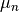$\mu_n$ . The clusters are updated to contain the closest points in distance to each centroid as it is described by the equation: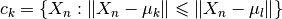

$c_k = \left \{ X_n:\left \| X_n -\mu_k \right \| \leqslant \left \| X_n - \mu_l \right \|\right \}$
The upadate step, given a set of clusters, recalculates the centroids as the means of all points belonging to a cluster:

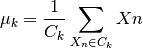
$\mu_k = \frac{1}{C_k}\sum _{X_n\in C_k} Xn$

The k-means algorithm loops through the two previous steps until the assignments of clusters and centroids no longer change. The convergence is guaranteed but the solution might be a local minimum as shown in the next equation:

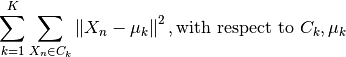
$\sum _{k=1}^K\sum _{X_n\in C_k}\left \| X_n - \mu_k \right \|^2 , \text{with respect to } C_k, \mu_k$

Parameters:	img (2d numpy array) – a slice of the toy model = 3 # number of clusters (n_clusters) – void, aggregate and mastic

:type int :param boolean normalize: If it is true, the segmentation mark the three

group of values as 0, 1 and 2. If it is false, the marks are the default values generated by k-means.

Returns:	the image segmented, with only three different possible values
Return type:	3d numpy array

segment_all_samples(samples)[source]¶

Take the given samples, uses K-Means algorithm with each sample slice and returns all the segmented samples. it also cuts irrelevant data corresponding to voids outside of the lenth of the radius of the toymodel

Parameters:	samples (list of 2d numpy arrays) – the set of slices of the toy model
Returns:	the toy model with its materials classified in airvoids, mastic and aggregates.
Return type:	list of 2d numpy arrays

app.imgprocessing.slice_mask.sector_mask(shape, centre=(50, 50), radius=50, angle_range=(0, 360))[source]¶

This method provides a circular mask over a numpy array (image), its purpose is to differentiate the air void pixels within the cylindrical toymodel from the air void space outward.

Parameters:	shape (two-dimensional tuple of integers) – shape of the image centre (two-dimensional tuple of integers) – point from where the circular mask is applied radius (float) – length of the radius for the circular mask angle_range (two-dimensional tuple of integers) – circular sector where the mask is applied, the whole circle by default
Returns:	mask for a circular sector
Return type:	2d boolean numpy array